There is a classic synthesizer from the 80’s, the 1984 Casio CZ-101. It has a special sound directly related to an innovative technique used in the creation.

One of the things that gave it a distinctive sound was the phase distortion synthesis. Phase distortion synthesis is similar to phase modulation and was used to simulate a resonant filter. This is super useful to be able to make iconic filter sweeps.

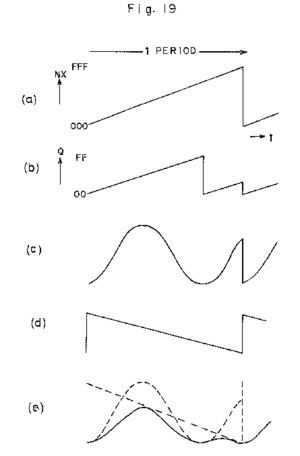
Basically it was done using a digital hard sync, by multiplying a hard synced signal against the inverted counter to level out the final signal. It is well described in Casio Computer Co Ltd patent filed in 1983:

It turns out it’s quite easy to generate this plot, pretty much exactly, just using SuperCollider code.

(
{
	var freqBase=100;
	var freqRes=130;
	var pdbase=Impulse.ar(freqBase);
	var pd=Phasor.ar(pdbase,2*pi*freqBase/s.sampleRate,0,2*pi);
	var pdres=Phasor.ar(pdbase,2*pi*freqRes/s.sampleRate,0,2*pi);
	var pdi=LinLin.ar((2*pi-pd).max(0),0,2*pi,0,1);
	[pd/(2*pi),pdres/(2*pi),SinOsc.ar(0,pdres),pdi,Lag.ar(SinOsc.ar(0,pdres)*pdi,1/freqBase)];
}.plot(0.011)
)

The code above results in a SuperCollider plot that looks eerily similar to the patent figure.

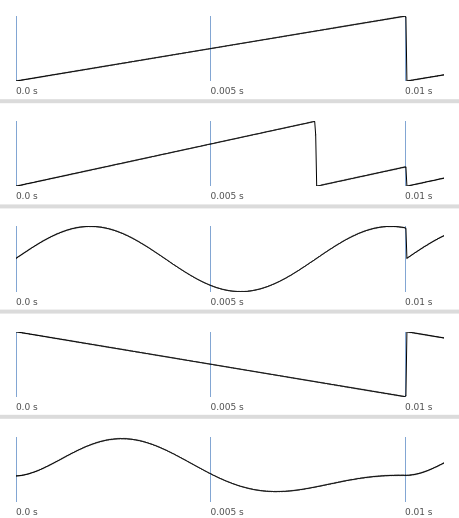
Now we can take that code and put it into a synth, and we have a re-creation of one small part of the Casio keyboard from 1984.

(
Routine {
	SynthDef("casioish",{
		arg freq=220, amp=0.5;
		var freqBase=freq;
		var freqRes=SinOsc.kr(Rand(0,0.2),0).range(freqBase/2,freqBase*2);
		var pdbase=Impulse.ar(freqBase);
		var pd=Phasor.ar(pdbase,2*pi*freqBase/s.sampleRate,0,2pi);
		var pdres=Phasor.ar(pdbase,2*pi*freqRes/s.sampleRate,0,2pi);
		var pdi=LinLin.ar((2pi-pd).max(0),0,2pi,0,1);
		var snd=Lag.ar(SinOsc.ar(0,pdres)*pdi,1/freqBase).dup;
		snd=Splay.ar(snd);
		snd=snd*EnvGen.ar(Env.perc(0.005,10));
		Out.ar(0,snd*amp);
	}).add;
	s.sync;

	x = Synth("casioish",[\freq,60.midicps]);
	y = Synth("casioish",[\freq,62.midicps]);
	z = Synth("casioish",[\freq,65.midicps]);
	w = Synth("casioish",[\freq,60.midicps/2,\amp,1.0]);
}.play
)

And here’s an example of the resulting sound: