There is a classic synthesizer from the 80’s, the 1984 Casio CZ-101. It has a special sound directly related to an innovative technique used in the creation.
One of the things that gave it a distinctive sound was the phase distortion synthesis. Phase distortion synthesis is similar to phase modulation and was used to simulate a resonant filter. This is super useful to be able to make iconic filter sweeps.
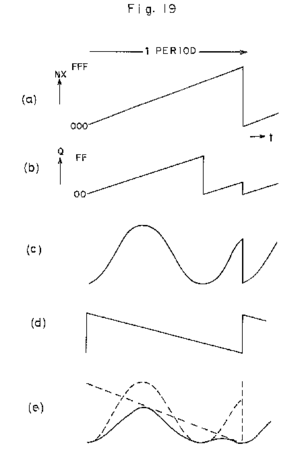
Basically it was done using a digital hard sync, by multiplying a hard synced signal against the inverted counter to level out the final signal. It is well described in Casio Computer Co Ltd patent filed in 1983:

It turns out it’s quite easy to generate this plot, pretty much exactly, just using SuperCollider code.
(
{
var freqBase=100;
var freqRes=130;
var pdbase=Impulse.ar(freqBase);
var pd=Phasor.ar(pdbase,2*pi*freqBase/s.sampleRate,0,2*pi);
var pdres=Phasor.ar(pdbase,2*pi*freqRes/s.sampleRate,0,2*pi);
var pdi=LinLin.ar((2*pi-pd).max(0),0,2*pi,0,1);
[pd/(2*pi),pdres/(2*pi),SinOsc.ar(0,pdres),pdi,Lag.ar(SinOsc.ar(0,pdres)*pdi,1/freqBase)];
}.plot(0.011)
)
The code above results in a SuperCollider plot that looks eerily similar to the patent figure.

Now we can take that code and put it into a synth, and we have a re-creation of one small part of the Casio keyboard from 1984.
(
Routine {
SynthDef("casioish",{
arg freq=220, amp=0.5;
var freqBase=freq;
var freqRes=SinOsc.kr(Rand(0,0.2),0).range(freqBase/2,freqBase*2);
var pdbase=Impulse.ar(freqBase);
var pd=Phasor.ar(pdbase,2*pi*freqBase/s.sampleRate,0,2pi);
var pdres=Phasor.ar(pdbase,2*pi*freqRes/s.sampleRate,0,2pi);
var pdi=LinLin.ar((2pi-pd).max(0),0,2pi,0,1);
var snd=Lag.ar(SinOsc.ar(0,pdres)*pdi,1/freqBase).dup;
snd=Splay.ar(snd);
snd=snd*EnvGen.ar(Env.perc(0.005,10));
Out.ar(0,snd*amp);
}).add;
s.sync;
x = Synth("casioish",[\freq,60.midicps]);
y = Synth("casioish",[\freq,62.midicps]);
z = Synth("casioish",[\freq,65.midicps]);
w = Synth("casioish",[\freq,60.midicps/2,\amp,1.0]);
}.play
)
And here’s an example of the resulting sound: